Принцип Діріхле

Розглянемо таку задачу.

Задача 1. У хвойному лісі росте 800000 ялин. На кожній ялині - не більше 500000 голок. Довести, що існують хоча б дві ялини з однаковою кількістю голок.

Розв'язування. Припустимо протилежне, тобто, припустимо, що в цьому лісі не існують дві ялини з однаковим числом голок. Тоді існує не більше однієї ялини (одна ялина або жодної), що має одну голку. Аналогічним чином, існує не більше однієї ялини з двома голками і т. д., не більше однієї ялини з 499999 голками, не більше однієї ялини з 500000 голками. Таким чином, не більше 500000 ялин володіють кількістю голок від 1 до 500000. Оскільки всього росте 800000 ялин, і кожна ялина має не більше 500000 голок, випливає, що знайдуться хоча б дві ялини з однаковим числом голок.

Зауваження. Легко помітити, що розв'язок в принципі не залежить від конкретних чисел 800000 (кількість ялин) і 500000 (найбільше число голок). Принципово був використаний той факт, що число 800000 строго більше 500000. У доказі передбачалося, що немає жодної ялини без голок, хоча завдання і доказ справедливі і в цьому випадку.

Тепер сформулюємо принцип Діріхле.

Нехай в n коробок поміщені k предметів. Якщо кількість предметів більша кількості коробок (k > n), тоді існує хоча б одна коробка, в якій знаходиться 2 предмети.

Зауваження. Зазначимо, що не важливо, в якій саме коробці знаходяться принаймні два предмети. Також не має значення, скільки предметів у цій коробці, і скільки всього таких коробок. Важливо те, що існує хоча б одна коробка з не менш, ніж двома предметами (два або більше).

У літературі цей принцип також зустрічається під назвами: "принцип кроликів і клітин", "принцип ящиків і об'єктів". 

Повернемося до задачі 1 та розв'яжемо її, використовуючи принцип Діріхле. Нехай є 500000 коробок, відповідно пронумерованих числами 1,2,3,...,500000. Розміщуємо (подумки) в ці коробки 800000 ялин наступним чином: в коробці з номером ѕ розміщуємо ялини, на яких рівно s голок. Оскільки ялин, тобто "предметів", більше, ніж коробок, випливає, що принаймні одна коробка буде містити не менш двох предметів, тобто, не менше двох ялин. Оскільки в одній і тій самій коробці знаходяться ялини з однаковим числом голок, приходимо до висновку, що існують хоча б дві ялини з однаковим числом голок. Звичайно, задача 1, як ми переконалися, очевидна, і легко може бути вирішена без допомоги принципу Діріхле. Тому, природно, виникає питання: "Для чого тоді потрібен принцип Діріхле?" Надалі ми побачимо, що деякі завдання не такі очевидні при безпосередньому розв'язанні, але в той самий час досить просто розв'язуються за принципом Діріхле. Простота розв'язку в значній мірі залежить від того, наскільки вдало будуть обрані "коробки" і "предмети". Тобто, при використанні принципу Діріхле необхідно вказати, що (хто) буде "коробкою", а що (хто) - "предметом".

Надалі, для закріплення матеріалу, розглянемо ряд завдань.

Задача 2. Довести, що серед шести цілих чисел знайдуться два числа, різниця яких ділиться на 5.

Розв'язування. Розглянемо 5 коробок, пронумерованих 0,1,2,3,4, - цифрами, що є залишками від ділення на 5. Розподілимо в ці коробки шість довільних цілих чисел у відповідності з залишком від ділення на 5, тобто в одну і ту ж коробку поміщаємо числа, що мають однаковий залишок від ділення на 5. Оскільки чисел ("предметів") більше, ніж коробок, за принципом Діріхле, існує одна коробка, що містить більше одного предмета. Тобто, існують (принаймні) два числа, поміщені в одну і ту ж коробку. Отже, існують два числа з однаковими залишками від ділення на 5. Тоді, різниця цих чисел ділиться на 5.

Задача 3. Довести, що для будь-якого натурального числа n ≥ 1, існує натуральне число, що складається з цифр 0 і 5, яке ділиться на n.

Розв'язування. Розглянемо натуральні числа

і розподілимо ці "предмети" в "коробки" пронумеровані 0,1,...,n-1 (цифрами, що є залишками від ділення на n). У коробку s поміщаємо число ak, яке має залишок від ділення на n, рівний s. Якщо в коробці з номером 0 знаходиться один "предмет" (тобто, одне число), тоді задача розв'язана. В іншому випадку n "предметів" знаходяться в n-1 "коробках". За принципом Діріхле, є два "предмета" (числа), що знаходяться в одній і тій самій коробці. Тобто, існують два числа, що мають однаковий залишок від ділення на n. Їх різниця буде ділиться на n, і як легко помітити, різниця чисел, які складаються з цифр 0 і 5, також буде числом, що складається з 0 і 5.

Задача 4. У залі перебувають n осіб (n ≥ 2). Довести, що серед них знайдуться дві людини з однаковим числом знайомих (передбачається, що якщо людина A є знайомою людини B, то B є знайомою A; ніхто не вважається своїм знайомим).

Розв'язування. Позначимо через m кількість осіб, які мають хоча б одне знайомство в залі (це і будуть "предмети"). Кожен з цих m людей може мати 1,2,...,m-1 знайомих ("коробки" - число знайомих). За принципом Діріхле, існує дві людини з однаковим числом знайомих. При розв'язуванні деяких завдань корисно застосовувати узагальнений принцип Діріхле. Якщо pn+1 предметів помістити n коробок, тоді хоча б одна коробка буде містити принаймні p+1 предметів.

Задача 5. В будинку живуть 40 учнів. Чи існує такий місяць, в якому хоча б 4 учні святкують свій день народження. 

Розв'язування. Нехай "коробками" будуть місяці, а "предметами" - учні. Розподіляємо "предмети" по "коробках" в залежності від місяця народження. Оскільки число місяців, тобто, коробок, дорівнює 12, а кількість учнів, тобто, предметів 40 = 12·3+4 за принципом Діріхле існує коробка (місяць) з принаймні 3+1=4 предметами (учнями). 

Задача 6. Нехай M - множина, що складається із n цілих чисел. Доведіть, що існує підмножина  M₁ множини M така, що сума елементів множини M₁ ділилася б на n.

Розв'язування. Нехай M = {a₁,a₂,...,a_n}. Розглянемо наступні суми

S1 = a1,

S2 = a1 + a2,

...

Sn = a1 + a2 + ... + an.

Якщо одне із чисел S_k (k = 1,...,n) не ділиться на n, тоді остачі від ділення на n будуть 1, 2, ..., n - 1. Оскільки є n сум і n - 1 остача, то принаймні дві суми дадуть однакову остачу при діленні на n. Нехай S_k і S_m (1 ≤ k < m ≤ n) - дві з них. Тоді S_m - S_k ділиться на n, і шукана множина буде {a_k+1,...,  a_m}.

Задача 7. Довести, що із n+1 різних натуральних чисел, менших за 2n, можна вибрати 3 числа так, щоб одне число дорівнювало б сумі двох інших.

Розв'язування. Нехай a₁ < a₂ < ... < a_n+1 - дані числа. Розглянемо різниці

a2 - a1,

a3 - a1,

...

an+1 - a1.

Ці числа різні, додатні і менші за 2n. За принципом Діріхле, хоча б два числа співпадають. Більш того, одне з цих чисел належить множині {a₂ - a₁, ... ,a_n+1 - a₁}. Нехай це будуть числа a_k і a_m - a₁. Звідки a_k = a_m - a₁, і, відповідно, a_m = a_k + a₁.

Задача 8. Нехай a₁, a₂, ... , a_n - перестановка чисел 1,2,3,...,n. Доведіть, що добуток (a₁ - 1)(a₂ - 2)...(a_n - n) буде парним, якщо n - непарне.

Розв'язування. Нехай n = 2k + 1. На множині розглянутих чисел k + 1 чисел будуть непарними. В даному добутку серед зменшуваних і від'ємників будуть (k + 1) + (k + 1) = 2(k + 1) = n + 1 непарних чисел. Оскільки добуток складається із n множників, один (принаймні) із них буде містити тільки непарні числа (і зменшуване та від'ємник будуть непарними). Таким чином, цей множник буде парним, і добуток також буде парним.

Задача 9. В 500 корзинах лежать яблука. Відомо, що в кожній корзині знаходяться не більше 240 яблук. Довести, що існують хоча б 3 корзини, які містять однакову кількість яблук. 

Розв'язування. Нехай у перших 240 корзинах знаходиться різна кількість яблук (1,2,...,240), в наступних 240 корзинах - аналогічно (тобто, аналізується екстремальний випадок; більш докладно про цей метод розповідається в темі "принцип крайнього"). Таким чином, залишилися 500 - 2·240 = 20 корзин, в які необхідно помістити яблука від 1 до 240. 

Задача 10. У коробці лежать 10 червоних олівців, 8 синіх, 8 зелених і 4 жовтих. Навмання (довільно) з коробки виймають n олівців. Визначити найменше число олівців, які необхідно вийняти, щоб серед них було:
a) не менше 4 олівців одного кольору;
b) по одному олівцю кожного кольору;
c)хоча б 6 олівців синього кольору.

Розв'язування. a) Нехай вийняли 13 олівців. Оскільки у нас всього 4 кольори, за принципом Діріхле (олівці будуть "предметами", а кольори - "коробками"), принаймні 4 олівця будуть однакового кольору. Доведемо, що n = 13 є найменшим числом. З цією метою покажемо ситуацію, за якої умови завдання не виконуються. Наприклад, коли вийняті по 3 олівці кожного кольору (12 олівців). Зазначимо, що ця ситуація можлива, так як в коробці знаходиться не менше 3 олівців кожного кольору.

Випадки b) і с) розв'язуються аналогічно.

Задача 11. У міжнародному симпозіумі беруть участь 17 осіб. Кожен знає не більше трьох мов та будь-які два учасники можуть спілкуватися між собою. Довести, що хоча б три учасника, знають одну й ту саму мову.

Розв'язування. Нехай A - один з учасників. Він може спілкуватися з кожним із 16 учасників на одному з трьох відомих йому мов. Тоді існує мова, на якій A розмовляє з не менш ніж шістьма учасниками. Нехай B - будь-який з них. Ясно, що серед решти 5 учасників є 3, з якими B може спілкуватися на одній мові (назвемо її "друга мова"). Якщо серед цих трьох учасників хоча б два, скажімо C і D, можуть говорити на "другій мові", то B, C і D і є ті три людини, що говорять на одній мові. Деякі завдання, особливо геометричні, розв'язуються за допомогою принципу Діріхле в таких формулюваннях:

a) Якщо на відрізку довжиною l розташовані кілька відрізків, сума довжин яких більше l, тоді принаймні два відрізки мають спільну точку;

b) Якщо всередині фігури площею S розташовані фігури, сума площ яких більше S, тоді серед них існують хоча б дві фігури, що мають спільну точку;

c) Якщо фігури F₁,F₂, ... ,F_n (S₁,S₂, ... ,S_n  - відповідно їх площі) розташовані у фігурі F площею S і S₁ + S₂ + ... + S_n > kS, тоді k + 1 з фигур F₁,F₂, ... ,F_n

мають спільну точку.

Задача 12. Точки на площині розфарбовані двома кольорами. Показати, що існують дві точки однакового кольору, розташовані на відстані 1м.

Розв'язування. Розглянемо рівносторонній трикутник зі стороною 1м. Вершини трикутника будуть "предметами", а кольори - "коробками". Так як число "предметів" більше числа "коробок", випливає, що існують дві вершини одного кольору. Оскільки трикутник рівносторонній, відстань між вершинами становить 1м. Зазначимо, що ця задача може бути розв'язана і іншим способом - методом від супротивного. Нехай А - одна з точок площини, і припустимо, що всі точки площини, розташовані на відстані 1м від A, пофарбовані в колір, відмінний від кольору точки A. Тоді отримуємо коло радіуса 1 з точок однакового кольору. Очевидно, що в цьому колі існує хорда довжиною 1м. Отже, кінцями хорди будуть точки одного кольору, розташовані на відстані 1м.

Задача 13. На площині дано n різних точок. Пара точок визначає відрізок. Довести, що існують дві точки, з яких виходить однакове число відрізків.

Розв'язування. З однієї точки може виходити максимум n - 1 відрізків і мінімум 1 відрізок. Оскільки є n точок, то знайдуться дві такі, з яких виходить однакове число відрізків.

Задача 14. Усередині квадрата зі стороною 1 знаходяться кілька кіл, сума довжин яких дорівнює 10. Показати, що існує пряма, що перетинає не менше чотирьох з цих кіл. .

Розв'язування. Проектуємо кола на одну зі сторін квадрата. Проекція кожного кола представляє собою відрізок, довжина якого дорівнює діаметру відповідного кола. Сума цих відрізків дорівнює  За принципом Діріхле, існують хоча б чотири відрізка, що мають спільну точку. Перпендикуляр, проведений із цієї точки на сторону квадрата, перетне не менше чотирьох кіл. 

Задача 15. Всередині рівностороннього трикутника зі стороною 1 лежать 5 точок. Довести, що знайдуться дві точки з п'яти, відстань між якими менше 0,5.

Розв'язування. Ділимо рівносторонній трикутник зі стороною 1 на чотири рівносторонніх трикутника зі стороною 0,5 (рис. 1).

В одному з цих чотирьох трикутників лежать принаймні дві з даних точок. Відстань між цими двома точками менше 0,5.

Задача 16. На площині дано 25 точок таким чином, що дві точки з будь-яких трьох розташовані на відстані менше 1. Довести, що існує круг радіуса 1, що містить не менше 13 з даних точок. 

Розв'язування.  Нехай A - одна з даних точок. Якщо інші точки знаходяться всередині круга S₁ радіуса 1 з центром у точці A, тоді задача розв'язана. Нехай B - одна з точок, що лежать поза кругом S₁. Розглянемо круг S₂ радіуса 1 з центром у точці B. Серед точок А, B, C, де C - довільна з даних точок, існують дві, відстань між якими менше 1. Більше того, цими точками не можуть бути A і B. Таким чином, круги S₁ і S₂ містять усі дані точки. Тобто, один з цих кругів містить не менше 13 точок.

Задача 17. На площині дано n попарно непаралельних прямих. Показати, що існують прямі, кут між якими становить менше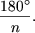 

Розв'язування. Вибираємо на площині точку, через яку проводимо прямі, паралельні даним n прямим. Ці прямі розбивають площину на 2n кутів, сума величин яких дорівнює 360°. Тобто, принаймні один з кутів буде меншим за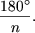   

Задача 18. На нескінченній сітці розміщена фігура, площа якої менше площі квадратика сітки. Довести, що ця фігура може бути розміщена на сітці так, щоб вона не покривала вузли сітки.

Розв'язування. Розміщуємо цю фігуру на сітці довільним чином і розрізаємо сітку вздовж сторін. Складаємо всі квадратики сітки один на інший, утворюючи стопку, при цьому здійснюючи тільки паралельні переміщення (без поворотів). Проектуємо фігуру на один квадратик. Проекції фігури не можуть покривати весь квадратик, так як його площа більше площі фігури. Повертаємося до початкового положення фігури і переносимо сітку паралельно, таким чином, щоб проекції вершин розташовувалися всередині фігури.В результаті ми отримаємо шукане положення фігури.